BOUSSOLE: Vicarious calibration

The top-of-the-atmosphere radiometric vicarious calibration is a challenging process, where high-quality data from several sources have to be put together, forming inputs to, and boudary conditions of, radative transfer calculations. This calculations are supposed to provide the top-of-the-atmosphere total radiance, to be compared to the same quantity as measured by the satellite-borne sensor. The principle of this calibration is exposed below, before a tentative performance budget is proposed and prelimianry results are shown for the MERIS sensor.

Principle

Two main vicarious calibration paths exist to produce ocean color products of the desired accuracy, i.e., water-leaving radiances within an uncertainty of about 5% in the blue for an oligotrophic ocean (Gordon 1997, and Antoine and Morel 1999). The first one is usually referred to as vicarious calibration, and consists in forcing the satellite-derived water-leaving radiances to agree with a set of in situ water-leaving radiances (match-up analyses). A set of vicarious calibration coefficients is obtained, which is applied to the top-of-atmosphere (TOA) total radiances measured by the sensor. The second procedure, which is also an indirect (vicarious) calibration is sometimes referred to as a vicarious radiometric calibration, and consists in simulating the TOA signal that the sensor should measure under certain conditions, and to compare it to the measured signal.

One of the difficulties of the first type of vicarious calibration is that it is dependent upon the procedure used for the atmospheric correction of the TOA observations. Even if it is admittedly less dependent upon the selected set of in situ water-leaving radiances, these measurements also contribute to the final accuracy. The advantage of this technique is, however, and besides the fact that atmospheric measurements are not needed, that the marine signals delivered by several sensors that use different atmospheric correction algorithms can be cross-calibrated provided that the same set of in situ waterleaving radiances is used to perform the vicarious calibration. This is presently the case, for instance, for the SeaWiFS and OCTS sensors.

Inconveniences of the vicarious radiometric calibration is that it requires a set of in situ measurements that is usually difficult to collect, among other things because a high accuracy is needed. In addition to the in-water measurements of the water-leaving radiances, this data set includes sea state and atmospheric pressure, ozone concentration, aerosol optical thickness, aerosol type, and even aerosol vertical profile if the aerosols reveal to be absorbing. If this data set is successfully assembled, the advantage of the vicarious radiometric calibration is that it is independent of the atmospheric correction algorithms, so that the TOA signals of various sensors can be cross-calibrated. Then it is up to any user to apply its preferred atmospheric correction to these TOA signals. The marine signals in that case might be inconsistent if significant differences exist in the various atmospheric corrections.

The greatest difficulty of the vicarious radiometric calibration lies in the estimation of the aerosol optical thickness, phase function, and single scattering albedo. These parameters are accessible through the inversion of sun photometer measurements, yet uncertainties inevitably occur when applying such methods, for instance because of multiple scattering, of perturbations from the ground reflectance, of uncertainties in the photometer calibration. Assembling all data needed for these vicarious calibration experiments are often compromised only because aerosol parameters are not accurate enough. The principle is illustrated on Fig. 35 A practical example will be provided later on (Sects. 10.3 and 10.4).

The Rayleigh scattering above clear waters method actually follows the same principle as the full radiometric vicarious calibration (the scheme displayed just above), but by using assumptions about, instead of measurements of, the various input parameters. This is particularly critical for the water-leaving radiances and the aerosol parameters. The final accuracy of this method cannot be better than that of the vicarious calibration procedure, except in a situation where the measurements used in the latter would be of very poor quality (or even erroneous).

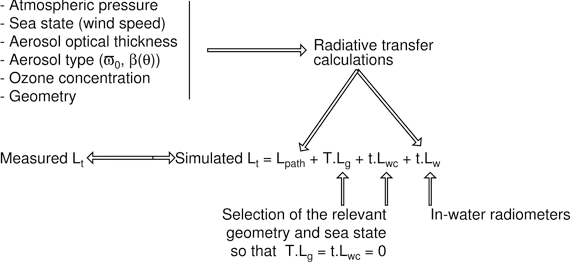
Overall logic of the top-of-the-atmosphere vicarious radiometric calibration of ocean color sensors. L stands for radiance, and the subscript “t” is for total (TOA), “G” for sun glint, “wc” for white caps, and “w” for water-leaving; “T” and “t” and the direct and diffuse atmospheric transmittances, respectively.

⁹The true, direct, calibration in principle consists in measuring the signal from a well-known standard, and is performed before launch for space-born sensors. After launch, only indirect (vicarious) procedures are possible.

¹⁰Except in situations where the atmosphere would be significantly different from the atmosphere present when performing the in situ measurements used for the vicarious calibration exercise.

¹¹When these measurements are not available and are replaced by averaged, reasonably estimated, values, the radiometric calibration here described comes down to the so-called Rayleigh calibration (or calibration over the Rayleigh), also planned within the frame of MERIS calibration and validation issues.

Performance budgets

It is in practice impossible to establish an a priori full performance budget, which should account for both unpredicted or unknown experimental sources of error (such as unidentified calibration deficiencies, difficulties encountered at sea, etc.) and theoretical limitations of the measurements themselves. The former are not totally known before starting the measurement sessions.

The budget presented below is therefore a tentative one, and any number provided in terms of percent error should be considered with caution. When the information necessary to confidently estimate the contribution of a given process to the error budget was missing or insufficiently known, this contribution has been assigned a somewhat optimistic value.

Each term that may have some impact on the modeling of the total radiance at the top of the atmosphere ), which is the sum of the atmospheric path radiance ( ) and of the product of the water-leaving radiance () by the atmospheric diffuse transmittance (), is examined below. At the end, the uncertainties on all terms are considered as random, Gaussian distributed, independent one of each other, so that the final error budget is computed as the square root of the sum of the squares of the individual error terms. The extent to which deviation from this hypothesis may impair the correctness of the final error budget has not been assessed.

Performance budgets: In-water measurements

The routine operations on the BOUSSOLE buoy should provide the measurements of , , and (nadir) at 5 and 9m. The basic operation consists of estimating the water-leaving radiance, from these in-water measurements, and in particular from . Evaluation of above-water techniques for the measurement of will be also tentatively set up (using a SIMBADA instrument), and will be examined later (Sect. 10.2.2).

The uncertainty to which Lu is measured is now considered as being of the order of 5% when carefully performing the measurements with well-calibrated instruments.

Extrapolation to null depth:
Here the problem is to compute the diffuse attenuation coefficient for the radiance along the nadir direction, , from the measurements performed at two depths on the buoy (nominally 5 and 9m); let us refer to it as . This value of is in principle used to compute the upwelling nadir radiance just below the surface, , through

where is about 5m.

Three important points intervene here, namely the intercalibration of the instruments at the two depths, which is assumed to be properly established, the correct estimation of the depth of the measurements, and finally the representativity of to perform the extrapolation of from 5m to just below the sea surface.

For clear waters (i.e., about 0.02m in the blue), a large uncertainty of 1m on the exact depth of measurement would lead to an error equal to , i.e., a 2% uncertainty on the estimation of . Conversely, if it is assumed that is correctly estimated, an uncertainty of 10% on would lead to an uncertainty equal to , i.e., an uncertainty of 1% (resp. 2%) on if is taken equal to 5m (resp. 10m). These numbers become 2.5% and 5% for , i.e., for mesotrophic waters, also typical of the BOUSSOLE site when the chlorophylla concentration reaches about 0.3mgm. What does ``resp.'' stand for?

The attenuation coefficient for the upwelling nadir radiance is known to vary a bit within the very upper layers of the ocean (2-5m), so that it is timely to examine whether or not remains the relevant coefficient to perform the extrapolation of measured at 5m to the level. The results of radiative transfer computations (Hydrolight code) show that a maximum difference of 5% exists between and for a chlorophylla concentration of 0.3mgm and a solar zenith angle of 45, which translates into a maximum error in of 1.25% when using KL,5-9 to perform the extrapolation, and when is about 0.05m (i.e., a chlorophylla concentration of 0.3mgm). This error could be significantly reduced by correcting the values of following what can be learned from the results of radiative transfer computations.

At the end, assuming an average error of 3% on the estimation of , because of uncertainties in the extrapolation to the level, seems realistic.

¹²The distance between the 2 depths of measurements is exactly known ; the depth in question here is that depth Z from which the extrapolation to just below the surface is performed through : Lu(0-) = Lu(Z) exp(KL . Z).

Bidirectional and transmission effects:
The in-water measurements provide the upwelling radiance at nadir, which has to be transformed into the upwelling radiance for the direction below water ( ) corresponding to an above-water zenith angle (), itself corresponding to a given viewing angle from the satellite, . The transformation is simply performed by ratioing the -factor at nadir to the -factor for the direction . The uncertainty is here only in the relative values of at these two directions (in a match-up configuration, the difference between both will be minimized, i.e., ). In the blue, where the geometry of the light field is not much depending on the particle phase function, the ratio of the -factors is probably correct within a very few percents; a 2% uncertainty will be assumed here.

The last step to get the water-leaving radiance is to multiply by the expression , which accounts for the transmission across the interface, where is the Fresnel reflection coefficient for the water-air interface and is the refractive index of water. This step does not introduce any error as far as and the sea surface is approximately flat (wind speed less than 15kts).

Atmospheric transmittance :
The water-leaving radiance, , has to be multiplied by the atmospheric diffuse transmittance, , before it can be added to the atmospheric path radiance. If the expression in use for computing are considered as valid (Wang 1999), the largest source of uncertainty is the aerosol optical thickness, which has a small impact on . A factor of two in (from 0.1 to 0.2) translates as a 2% error on at 443nm, which means a 2% uncertainty on the product .

In the green domain ( nm), another source of uncertainty is the ozone content of the atmosphere. When nm, the Rayleigh optical thickness is about 0.09 and the ozone optical thickness is about 0.03 for an ozone content of 350DU. The uncertainty in corresponding to an uncertainty of 50DU would be of the order of 0.5% for viewing angles less than 45 (with, for instance, .

Above-water measurements

The uncertainty to which is derived from the radiance measured above the sea surface (which includes and surface reflection effects), is now considered as being of the order of 10% (Hooker et al. 2002; Hooker and Morel 2003), at least when performed in well-controlled experimental conditions and in excellent environmental conditions. Because the measurements are taken from above the sea surface, the uncertainty attached to the extrapolation of in-water measurements from depth to just beneath the surface does not enter into account here. The same uncertainty is attached to the determination of bi-directional effects (Q factors) as well as to the calculation of the atmospheric diffuse transmittance.

Atmospheric path radiance

The uncertainties when calculating the atmospheric path radiance are now examinea, as originating from the uncertainties on the various parameters entering into its computation.

Atmospheric pressure :

Atmospheric pressure, , is known to better than 0.5% (i.e., 5hPa). The changes in the path reflectance due to changes in can be expressed as (Antoine and Morel 1998):

where is the ratio of the Rayleigh optical thickness to the total (i.e., aerosol plus Rayleigh) optical thickness. In the worst situation, where (no aerosols), the error in is directly transferred onto (it is actually a little less (Gordon et al. 1988). It will be also less as soon as the AOT is not zero. A 0.2% uncertainty is assumed here when the atmospheric pressure is known (local measurements from the meteo buoy in the vicinity of the BOUSSOLE site).

Sea surface state :
Quantification of the uncertainty due to an incorrect representation of the sea surface state is not really possible, and it would be probably useless because of the large uncertainties that remain in the parameterization of the surface wave slope probability distribution as a function of the wind speed. A tentative value of 0.5% is assumed here for the uncertainty introduced by these surface effects in the computation of at the TOA level, with the underlying assumption that experiments are only performed for days of calm weather.

Aerosol optical thickness :
The AOT should be known to better than 0.01 in absolute units (Fargion and Mueller 2000). The relative changes in due to changes in AOT in the blue and green domains (i.e., around 440 and 550nm, respectively), , are of the order of 0.1, e.g., see Fig. 5 in Antoine and Morel (1998). An uncertainty of 0.01 in should, therefore, translate as an uncertainty of 0.001 in , which corresponds to about 1% of when , and to about 2% of for the same value of the AOT. The uncertainties are slightly less as soon as is greater. These two values (1% and 2%) are taken here. Note that the corresponding numbers become 2-3% at 865nm.

Aerosol type :

Retrieving the aerosol type, actually the aerosol volume scattering function (VSF) and single scattering albedo, is much more difficult than retrieving the AOT: firstly because the retrieval is based on inversion of sky radiance measurements, which are delicate to perform with the desired calibration constraints, and, secondly, because the inversion itself necessarily uses assumptions and is also subject to uncertainties.

In order to minimize the impact of uncertainties on the aerosol type, situations where the satellite data and external information (wind direction, independent observations, etc.) are both available will be selected, in such a way that there is every chance of being in presence of maritime aerosols. Note that information about the relative humidity (RH) at the sea level will be available from the measurements of the meteo buoy located in the vicinity of the BOUSSOLE mooring. =Table15.tex;''

It is, therefore, considered here that the uncertainty is entirely due to the uncertainty on RH (the value itself or the vertical profile), for maritime aerosols conforming to the description of Shettle and Fenn (1979). From the results of radiative transfer simulations performed with these models, it appears that an uncertainty of 15% in the relative humidity (RH equal to 70% or 99% instead of 80%) leads to a 2% uncertainty in the computation of when and . This uncertainty is closer to 5% in the NIR (nm).

Maintaining this level of uncertainty means that the vicarious calibration experiments have to be performed for values as low as possible and for high solar elevations (the minimum solar zenith angle at the BOUSSOLE site is about 21^o).

Ozone content :

The importance of ozone content investigated here is its effect on the calculation of (the other effect has been already considered in the calculation if the atmospheric diffuse transmittance). Ozone does not strongly affect the blue bands, which are the most critical for ocean color. A null impact on is considered here.

For the green band, the problem is different because the ozone absorption is there at its maximum, with an optical thickness of about 0.03 at 550nm when the total ozone amount is equal to 350DU. The impact on remains, however, extremely weak, i.e., less than a 5% difference between for an atmosphere with a standard ozone amount (350DU) and an ozone-free atmosphere. The typical uncertainties in the ozone amount (i.e., 20DU) should, therefore, be without significant impact on the computation of (less than 0.5%).

The calibration uncertainty has been already considered when examining the uncertainty due to incorrect determination of the AOT and aerosol type.

In principle, a valid radiative transfer code, when fed with accurate inputs, provides an exact answer in terms of radiance. It is, therefore, assumed that the modeling itself does not introduce any additional uncertainty.

Marine contribution to total radiance

In clear oligotrophic waters, reaches its maximum in the blue, and corresponds to about 15% of the TOA total radiance at 440nm when the AOT is 0.05. Conversely, experiences minimum values in the green, and corresponds for instance to about 5% of the TOA total radiance at 550nm when the AOT is 0.3. Consequently, the various uncertainties in the estimation of as given above in terms of percentages , correspond to errors in ranging from % to %.

The various terms are summarized in the tables below, and following three different configurations concerning the estimation of the marine and atmospheric contributions to the TOA total radiance: inwater measurements of and measurements of the aerosol properties, above-water measurements of and measurements of the aerosol properties, and, finally (and tentatively), estimate values for the water-leaving radiance and aerosol properties (the so-called Rayleigh scattering above clear water technique).

Conclusions :

In summary, the values in the tables below show that a 2-3% uncertainty in the simulation of the TOA total radiance can be reached in extremely favorable conditions. Considering the possible type and range of uncertainties that are possible, a more realistic estimate of the accuracy to which the vicarious calibration can be performed would be approximately 5% in the visible part of the spectrum.

A practical example

The inversion algorithm that is suggested in Sect. 7.6 not only permits the characterization of the micro-physical properties of the aerosols providing the refractive index, but also permits to have a knowledge on the aerosol phase function which is a key parameter in the estimation of the atmospheric radiance and transmittance. The proposed algorithm can thus be used to lead a vicarious calibration of ocean color sensors.

The focus here is on the vicarious calibration of MERIS in the NIR band at 865nm. The sun photometer (Sects. 3.3, 4.3, and 5.3) is used to provide the necessary information about the aerosol properties. The procedure for the vicarious calibration is outlined as follows:

The aerosol refractive index is derived with the inversion algorithm;
The optical depth and Angström exponent are measured; and
The top of atmosphere radiance is computed with the OSOA radiative transfer model for similar geometries of MERIS scenes on the basis of the aerosol optical properties, which is compared with the top of atmosphere signal recorded by MERIS.

Some restrictions and assumptions should be made, however, to apply the vicarious calibration technique:
The ocean is assumed to be black at 865nm which is realistic in the Mediterranean Sea (open ocean waters), so no marine signal was included in the computations;
The MERIS images were selected for geometrical conditions that permit to aim at the vicinity of the ground photometer avoiding the glint;
Because of the closeness of the land in each image, the aerosol properties may exhibit a strong spatial variability at the land-ocean interface, so the aerosol model derived from the coastal photometer will be applicable to MERIS marine pixels only if a spatial homogeneity of the aerosols is observed in the study area (this constraint is restrictive and substantially reduced the number of available satellite images for the calibration);
For each selected image, a subscene of 1010 pixels is extracted far enough from the coastline (typically at a distance greater than 6km) to avoid the adjacency effects on the radiance measured by the satellite sensor (Santer and Schmechtig 2000); and
After correction for the eccentricity of the Earth orbit, the top of atmosphere radiance is averaged over this sub-scene.

Rigorously, the inversion algorithm is applied on ground-based measurements collected at the time of the satellite overpass (around 1000GMT for the Villefranche site) so that the simulated radiance is consistent with MERIS data. Nevertheless, it happens that measurements are not available at the time of overpass; either they are missing or of bad quality. For such situations, the aerosol model derived from the inversion of the closest (in time) measurements of satellite overpass is used to reconstruct the top of atmosphere signal. This is possible provided that stable conditions are observed during the day. The daily variation of the Angström exponent is used to check this assumption.