Next: Freshwater budget and salinity increase
Up: Warming and freshwater budget change in the Mediterranean since the
Previous: Marine data and surface changes
From calculated or measured temperature changes in different layers and locations, the
change in the heat content of the Mediterranean Sea, d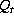 , amounts to a mean value of 0.65
, amounts to a mean value of 0.65 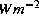 between 1940 and 1995 (derived from 0.70 and 0.53
between 1940 and 1995 (derived from 0.70 and 0.53 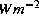 in the eastern and western
basin, respectively).
Changes in marine advection must be considered given the
temporal changes in deep water temperature and salinity as well as changes in
water deficit and flows. An
almost constant density of western deep-water means a constant deep outflow,
in the eastern and western
basin, respectively).
Changes in marine advection must be considered given the
temporal changes in deep water temperature and salinity as well as changes in
water deficit and flows. An
almost constant density of western deep-water means a constant deep outflow, 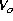 , while the
temperature of Atlantic inflow,
, while the
temperature of Atlantic inflow, 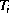 , is assumed constant. Using
, is assumed constant. Using 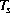 to approximate
to approximate 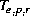 , temporal
changes in marine advection may be written as:
, temporal
changes in marine advection may be written as:
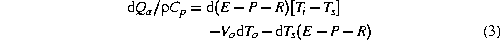
For an initial E - P - R = 2.38 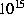 kg
kg 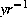 and a d(E - P - R) of 4.6
and a d(E - P - R) of 4.6 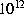 kg
kg 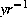 , the 20-box model
calculations give mean for
, the 20-box model
calculations give mean for 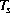 , d
, d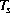 and d
and d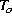 of 13.25
of 13.25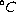 , 7.34
, 7.34 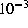
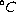
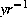 and 2.9
and 2.9 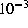
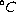
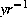 ,
respectively. The calculated temperature change in deep outflow, d
,
respectively. The calculated temperature change in deep outflow, d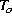 , is slightly lower than that
measured in the western deep waters, being 3.47
, is slightly lower than that
measured in the western deep waters, being 3.47 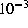
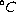
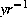 , due to vertical mixing in the
Alboran Sea between the Mediterranean outflow and the Atlantic inflow. The resulting advection
change, d
, due to vertical mixing in the
Alboran Sea between the Mediterranean outflow and the Atlantic inflow. The resulting advection
change, d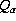 , over the 1940-1995 period amounts to: -0.44
, over the 1940-1995 period amounts to: -0.44 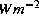 in 1995. The shift is linked
mainly to the temperature change in deep outflow (second term on the right-hand side of Eq.3).
In considering the initial driving force, 1.5
in 1995. The shift is linked
mainly to the temperature change in deep outflow (second term on the right-hand side of Eq.3).
In considering the initial driving force, 1.5 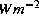 in 1995, part of this energy compensates for
the advection decrease, d
in 1995, part of this energy compensates for
the advection decrease, d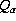 (-0.44
(-0.44 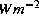 ), some of it contributes to an increase in the heat
content of the water column, d
), some of it contributes to an increase in the heat
content of the water column, d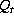 = 0.65
= 0.65 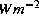 , while the remainder 0.41
, while the remainder 0.41 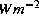 corresponds
to an increase in heat transferred towards the atmosphere by either evaporation, sensible heat
flux or longwave radiation. Inasmuch as there is no evidence of continuous changes in wind
speed and/or air humidity, the changes in heat transfers result from d
corresponds
to an increase in heat transferred towards the atmosphere by either evaporation, sensible heat
flux or longwave radiation. Inasmuch as there is no evidence of continuous changes in wind
speed and/or air humidity, the changes in heat transfers result from d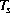 and d
and d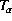 . From previous
studies of air-sea heat exchanges in the Mediterranean Sea, preliminary estimates of changes in air-sea
transfers driven by small changes in air and sea temperature were presented [Béthoux et al., 1990],
where:
. From previous
studies of air-sea heat exchanges in the Mediterranean Sea, preliminary estimates of changes in air-sea
transfers driven by small changes in air and sea temperature were presented [Béthoux et al., 1990],
where:
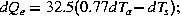
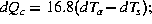
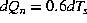 (with d
(with d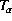 and d
and d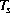 in
in
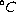 , and d
, and d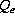 , d
, d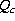 and d
and d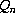 being in
being in 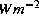 ). The sum gives:
). The sum gives:
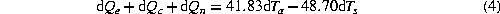
This sum was previously assumed equal to -0.41 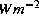 . With mean d
. With mean d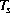 being previously
calculated equal to 7.34
being previously
calculated equal to 7.34 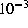
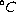
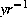 , Eq.4 can be used to calculate the mean change in air
temperature, giving d
, Eq.4 can be used to calculate the mean change in air
temperature, giving d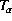 = 8.37
= 8.37 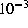
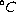
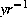 . This value is situated between the two estimates of
global trend calculated from available climatic data over the northern hemisphere since the
1960s: 6 and 10
. This value is situated between the two estimates of
global trend calculated from available climatic data over the northern hemisphere since the
1960s: 6 and 10 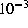
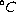
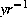 [Jones et al., 1988, Jones, 1994]. With known d
[Jones et al., 1988, Jones, 1994]. With known d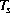 and d
and d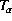 values, different changes in air-sea transfers may be calculated. For instance, the resulting
changes in 1995 ( when compared with transfers in 1940) for d
values, different changes in air-sea transfers may be calculated. For instance, the resulting
changes in 1995 ( when compared with transfers in 1940) for d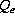 , d
, d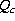 and d
and d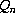 are equal to
-1.60, +0.95 and +0.24
are equal to
-1.60, +0.95 and +0.24 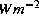 , respectively.
, respectively.
With the previous hypotheses of no change in the solar radiation, nor in the Atlantic advection, the
initial driving force of 1.5 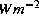 may correspond to a decrease of net longwave radiation due to
the change in atmospheric composition of radiative components. The calculated d
may correspond to a decrease of net longwave radiation due to
the change in atmospheric composition of radiative components. The calculated d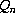 corresponds to a decrease of net longwave radiation due to the evolution of water temperature,
probably a feedback from the atmospheric effect. Consequently the total change in net
longwave radiation, i.e. the greenhouse effect increase, amounts to 1.5 + 0.24 = 1.74
corresponds to a decrease of net longwave radiation due to the evolution of water temperature,
probably a feedback from the atmospheric effect. Consequently the total change in net
longwave radiation, i.e. the greenhouse effect increase, amounts to 1.5 + 0.24 = 1.74 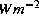 in the Mediterranean area over the 1940-1995 period.
in the Mediterranean area over the 1940-1995 period.
In the previous relationships for d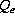 and d
and d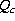 , numerical factors depend on the drag coefficient
(taken equal to 1.7
, numerical factors depend on the drag coefficient
(taken equal to 1.7 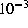 ), the mean wind speed (7.1 m
), the mean wind speed (7.1 m 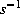 ) and air humidity (77% or 0.77, the
d
) and air humidity (77% or 0.77, the
d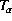 coefficient in d
coefficient in d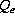 formula), which somewhat constrains the quantitative results.
Nevertheless, drag coefficient and wind speed act both on d
formula), which somewhat constrains the quantitative results.
Nevertheless, drag coefficient and wind speed act both on d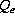 and d
and d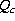 calculations and
consequently they have practically no effect on the calculation of d
calculations and
consequently they have practically no effect on the calculation of d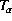 from d
from d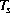 (Eq.4).
Similarly, a change of +/- 100% of the estimated sum ( d
(Eq.4).
Similarly, a change of +/- 100% of the estimated sum ( d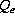 + d
+ d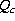 + d
+ d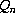 ), from a 30%
increase of either the external driving force (1.5
), from a 30%
increase of either the external driving force (1.5 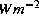 ) or the estimated d
) or the estimated d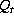 (0.65
(0.65 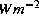 ), gives
new estimates of d
), gives
new estimates of d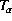 of 8.19 and 8.46
of 8.19 and 8.46 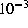
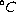
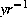 , respectively, i.e. rather low changes of -2%
and +1%. In order to have both an increase in evaporation (d
, respectively, i.e. rather low changes of -2%
and +1%. In order to have both an increase in evaporation (d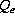 < 0, salinity increase) and a
decrease in sensible heat flux (d
< 0, salinity increase) and a
decrease in sensible heat flux (d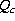 > 0,
> 0, 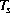 increase), sea surface temperature change d
increase), sea surface temperature change d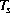 has to
be between two limits depending on air temperature change, d
has to
be between two limits depending on air temperature change, d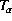 , and humidity,
, and humidity, 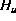 :
:
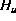 d
d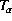 < d
< d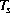 < d
< d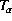 . This relationship illustrates that surface temperature change d
. This relationship illustrates that surface temperature change d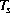 in the
Mediterranean is mainly driven by air temperature change d
in the
Mediterranean is mainly driven by air temperature change d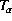 over the northern hemisphere.
over the northern hemisphere.
Next: Freshwater budget and salinity increase
Up: Warming and freshwater budget change in the Mediterranean since the
Previous: Marine data and surface changes
![]() may correspond to a decrease of net longwave radiation due to
the change in atmospheric composition of radiative components. The calculated d
may correspond to a decrease of net longwave radiation due to
the change in atmospheric composition of radiative components. The calculated d![]() corresponds to a decrease of net longwave radiation due to the evolution of water temperature,
probably a feedback from the atmospheric effect. Consequently the total change in net
longwave radiation, i.e. the greenhouse effect increase, amounts to 1.5 + 0.24 = 1.74
corresponds to a decrease of net longwave radiation due to the evolution of water temperature,
probably a feedback from the atmospheric effect. Consequently the total change in net
longwave radiation, i.e. the greenhouse effect increase, amounts to 1.5 + 0.24 = 1.74 ![]() in the Mediterranean area over the 1940-1995 period.
in the Mediterranean area over the 1940-1995 period.
![]() and d
and d![]() , numerical factors depend on the drag coefficient
(taken equal to 1.7
, numerical factors depend on the drag coefficient
(taken equal to 1.7 ![]() ), the mean wind speed (7.1 m
), the mean wind speed (7.1 m ![]() ) and air humidity (77% or 0.77, the
d
) and air humidity (77% or 0.77, the
d![]() coefficient in d
coefficient in d![]() formula), which somewhat constrains the quantitative results.
Nevertheless, drag coefficient and wind speed act both on d
formula), which somewhat constrains the quantitative results.
Nevertheless, drag coefficient and wind speed act both on d![]() and d
and d![]() calculations and
consequently they have practically no effect on the calculation of d
calculations and
consequently they have practically no effect on the calculation of d![]() from d
from d![]() (Eq.4).
Similarly, a change of +/- 100% of the estimated sum ( d
(Eq.4).
Similarly, a change of +/- 100% of the estimated sum ( d![]() + d
+ d![]() + d
+ d![]() ), from a 30%
increase of either the external driving force (1.5
), from a 30%
increase of either the external driving force (1.5 ![]() ) or the estimated d
) or the estimated d![]() (0.65
(0.65 ![]() ), gives
new estimates of d
), gives
new estimates of d![]() of 8.19 and 8.46
of 8.19 and 8.46 ![]()
![]()
![]() , respectively, i.e. rather low changes of -2%
and +1%. In order to have both an increase in evaporation (d
, respectively, i.e. rather low changes of -2%
and +1%. In order to have both an increase in evaporation (d![]() < 0, salinity increase) and a
decrease in sensible heat flux (d
< 0, salinity increase) and a
decrease in sensible heat flux (d![]() > 0,
> 0, ![]() increase), sea surface temperature change d
increase), sea surface temperature change d![]() has to
be between two limits depending on air temperature change, d
has to
be between two limits depending on air temperature change, d![]() , and humidity,
, and humidity, ![]() :
:
![]() d
d![]() < d
< d![]() < d
< d![]() . This relationship illustrates that surface temperature change d
. This relationship illustrates that surface temperature change d![]() in the
Mediterranean is mainly driven by air temperature change d
in the
Mediterranean is mainly driven by air temperature change d![]() over the northern hemisphere.
over the northern hemisphere.